O-species and tensor algebras

• BibTex
• RIS
• APA
• Harvard
• IEEE
• MLA
• Vancouver
• Chicago

@article{Gubareni_2016,
   doi = {10.17512/jamcm.2016.2.03},
   url = {https://doi.org/10.17512/jamcm.2016.2.03},
   year = 2016,
   publisher = {The Publishing Office of Czestochowa University of Technology},
   volume = {15},
   number = {2},
   pages = {23--30},
   author = {Nadiya Gubareni},
   title = {O-species and tensor algebras},
   journal = {Journal of Applied Mathematics and Computational Mechanics}
}

TY  - JOUR
DO  - 10.17512/jamcm.2016.2.03
UR  - https://doi.org/10.17512/jamcm.2016.2.03
TI  - O-species and tensor algebras
T2  - Journal of Applied Mathematics and Computational Mechanics
JA  - J Appl Math Comput Mech
AU  - Gubareni, Nadiya
PY  - 2016
PB  - The Publishing Office of Czestochowa University of Technology
SP  - 23
EP  - 30
IS  - 2
VL  - 15
SN  - 2299-9965
SN  - 2353-0588
ER  - 

Gubareni, N. (2016). O-species and tensor algebras. Journal of Applied Mathematics and Computational Mechanics, 15(2), 23-30. doi:10.17512/jamcm.2016.2.03

Gubareni, N., 2016. O-species and tensor algebras. Journal of Applied Mathematics and Computational Mechanics, 15(2), pp.23-30. Available at: https://doi.org/10.17512/jamcm.2016.2.03

[1]N. Gubareni, "O-species and tensor algebras," Journal of Applied Mathematics and Computational Mechanics, vol. 15, no. 2, pp. 23-30, 2016.

Gubareni, Nadiya. "O-species and tensor algebras." Journal of Applied Mathematics and Computational Mechanics 15.2 (2016): 23-30. CrossRef. Web.

1. Gubareni N. O-species and tensor algebras. Journal of Applied Mathematics and Computational Mechanics. The Publishing Office of Czestochowa University of Technology; 2016;15(2):23-30. Available from: https://doi.org/10.17512/jamcm.2016.2.03

Gubareni, Nadiya. "O-species and tensor algebras." Journal of Applied Mathematics and Computational Mechanics 15, no. 2 (2016): 23-30. doi:10.17512/jamcm.2016.2.03

O-SPECIES and TENSOR ALGEBRAS

Nadiya Gubareni

Institute of Mathematics, Czestochowa University of Technology
Częstochowa, Poland
nadiya.gubareni@yahoo.com

Abstract. In this paper we consider O-species and their representations. These O-species are a type of a generalization of a species introduced by Gabriel. We also consider the tensor algebras of such O-species. It is proved that the category of all representations of an O-species and the category of all right modules over the corresponding tensor algebra are naturally equivalent.

Keywords: species, O-species, representations of O-species, tensor algebra, O-species of bounded representation type, diagram of O-species

1. Introduction

In this paper we consider O-species, which generalize the notion of species introduced by Gabriel in [1]. Recall this definition:

Definition 1.1. (Gabriel [1]). Let I be a finite index set. A species L = (F_i, _iM_j)_{i,j Î I} is a finite family (F_i)_{i Î I} of division rings together with a family (_iM_j)_{i,j Î I} of (F_i, F_j)-bimodules.

We say that (F_i, _iM_j)_{i,j Î I} is a K-species if all F_i are finite dimensional and central over the common commutative subfield K which acts centrally on _iM_j, i.e. lm = ml for all l Î K and all m Î _iM_j. We also assume that each bimodule _iM_j is a finite dimensional vector space over K. K-species is a K-quiver if F_i = K for each i.

Definition 1.2. A representation (V_i, _jj_i) of a species L = (F_i, _iM_j)_{i,j Î I} (or an L-representation) is a family of right F_i-modules V_i and F_j-linear mappings:

(1.3)

for each i, j Î I. Such a representation is called finite dimensional, provided all the spaces V_i are finite dimensional vector spaces.

Let V = (V_i, _jj_i ) and W = (W_i,) be two L-representations. An L-morphism Y: V ® W is a set of F_i-linear maps a_i : V_i ® W_i such that

(1.4)

Two representations (V_i, _jj_i) and W = (W_i, _jy_i) are called equivalent if there is a set of isomorphisms a_i from the F_i-module V_i to the F_i-module W_i such that the (1.4) holds for all i,j Î I.

A representation (V_i, _jj_i) is called indecomposable, if there are no non-zero sets of subspaces (U_i) and (W_i) such that V_i = U_i Å W_i and _jj_i = _jy_i Å _jt_i , where

(1.5)

(1.6)

One defines the direct sum of two L-representations in the obvious way.

Denote by Rep(L) the category of all L-representations, and by rep(L) the category of finite dimensional L-representations, whose objects are L-representations and whose morphisms are as defined above.

Definition 1.7. [2] A species L = (F_i, _iM_j)_i,jÎI is said to be of finite type, if the number of indecomposable non-isomorphic finite dimensional representations is finite.

A species L = (F_i, _iM_j)_i,jÎI is said to be of strongly unbounded type if it possesses the following three properties:

1. L has indecomposable objects of arbitrary large finite dimension.

2. If L contains a finite dimensional object with an infinite endomorphism ring, then there is an infinite number of (finite) dimensions d such that, for each d, the species L has infinitely many (non-isomorphic) indecomposable objects of dimension d.

3. L has indecomposable objects of infinite dimension.

Dlab and Ringel proved in [2, Theorem E] that any K-species is either of finite or of strongly unbounded type.

With any species L = (F_i, _iM_j)_i,jÎI one can define the tensor algebra in the following way. Let , and let . Then B is a ring and M naturally becomes a (B, B)-bimodule. The tensor algebra of the (B, B)-bimodule M is the graded ring

(1.8)

with component-wise addition and the multiplication induced by taking tensor products.

If L is a K-species, then T(L) is a finite dimensional K-algebra.

Theorem 1.9. (Dlab, Ringel [2, Proposition 10.1]). Let L be a K-species. Then the category Rep(L) of all representations of L and the category Mod_r(T(L)) of all right T(L)-modules are equivalent.

2. O-species and their representations

In this section we consider the notion of O-species, which generalizes the notion of species considered in [1].

Let {O_i} be a family of discrete valuation rings (not necessarily commutative) O_i with radicals R_i and skew fields of fractions D_i, for i = 1, 2, ..., k, and let {D_j}, for j = k + 1, ..., n, be a family of skew fields. Let (n₁, n₂, ..., n_k) be a set of natural numbers. Write

,

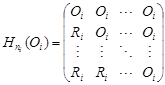which is a subring in the matrix ring . It is easy to see that each is a Noetherian serial prime hereditary ring. Write F_i = for i = 1, 2, ..., k, and F_j = D_j for j = k + 1, ..., n. Then, by the Goldie theorem, there exists a classical ring of fractions for i =1,2, ..., n.

Consider the following generalization of a species.

Definition 2.1. An O-species is a set W = (F_i, _iM_j)_{i,j Î I}, where F_i = for i = 1, 2, ..., k, and F_j = D_j for j = k + 1, ..., n, and moreover _iM_j is an -bimodule, which is finite dimensional as a right D_j-vector space and as a left D_i -vector space.

An O-species W is called a (D, O)-species if all O_i have a common skew field of fractions D, i.e. all D_i are equal to a fixed skew field D and

(2.2)

for some natural number n_ij (i = 1, 2, ..., n).

An O-species W is called a (K, O)-species, if all D_i (i = 1, 2, ..., n) contain a common central subfield K of finite index in such a way that lm = ml for all l Î K and all m Î _iM_j (moreover, each bimodule _iM_j is a finite dimensional vector space over K). It is a (K, O)-quiver if moreover D_i = D for each i.

Everywhere in this paper we will consider O-species without oriented cycles and loops, i.e. we will assume that _iM_i = 0, and if _iM_j ≠ 0, then _jM_i = 0. A vertex i is said to be marked if F_i = .

We will also assume that all marked vertices are minimal, i.e. _jM_i = 0 if F_i = , and that _iM_j = _jM_i = 0 if i, j are marked vertices.

Definition 2.3. The diagram of an O-species W = {F_i, _iM_j}_i,jÎI is defined in the following way:

1. The set of vertices is a finite set I = {1, 2, ..., n}.

2. The finite subset I₀ = {1, 2, ..., k} of I is a set of marked points.

3. The vertex i connects with the vertex j by t_ij arrows, where

moreover, we assume that n_i = 1 if F_i = D_i.

Similar to species we can define representations of O-species in the following way.

Definition 2.4. A representation (M_i, V_r, _jj_i, _jy_r) of an O-species W = {F_i, _iM_j}_i,jÎI is a family of right F_i-modules M_i (i = 1, 2, ..., k), a set of right vector spaces V_r over D_r (r = k +1, k +1, ..., n) and D_j-linear maps:

for each i = 1, 2, ..., k; j = k +1, k +2, ..., n; and

for each r, j = k +1, k +2, ..., n.

Definition 2.5. Two representations M = (M_i, V_r, _jj_i, _jy_r) and are called equivalent if there is a set of isomorphisms a_i of F_i-modules from M_i to and a set of isomorphisms b_r of D_r-vector spaces from V_r to such that for each i = 1, 2, ..., k; r, j = k + 1, k + 2, ..., n the following equalities hold:

(2.6)

(2.7)

In a natural way one can define the notions of a direct sum of representations and of an indecomposable representation.

The set of all representations of an O-species W = (F_i, _iM_j)_i,jÎI can be turned into a category R(W), whose objects are representations M = (M_i, V_r, _jj_i, _jy_r), and a morphism from object M = (M_i, V_r, _jj_i, _jy_r) to object is a set of homomorphisms a_i of - modules M_i to , and a set of homo- morphisms b_r of D_r - vector spaces from V_r to such that for each i = 1,2, ..., k; r, j = k + 1, k + 2, ..., n the equalities (2.6) and (2.7) hold.

3. Tensor algebra of O-species

For any O-species W = (F_i, _iM_j)_{i,j Î I} one can construct a tensor algebra of bimodules T(W). Let , . Then B is an (A, A) - bimodule and we can define a tensor algebra T_A(B) of the bimodule B over the ring A in the following way:

is a graded ring, where Bⁿ = B Ä_A B^n‒1 for n > 1, and multiplication in T_A(B) is given by the natural A-bilinear map:

Then T(W) = T_A(B) is the tensor algebra corresponding to an O-species W.

Proposition 3.3. Let W be an O-species. Then the category (W) of all representations of W and the category Mod_r T(W) of all right T(W)-modules are naturally equivalent.

Proof. Form two functors R: Mod_r T(W) ® (W) and P: (W) ® Mod_r T(W) in the following way. Let X_T(W) be a right T(W)-module. Since A is a subring in T(W), X can be considered as a right A-module. Then

(3.4)

where M_i is an -module, and V_r is a D_r-vector space; moreover, for i ≠ j, and V_rD_s = 0 for r ≠ s. Since B is an (A, A)-bimodule, one can define an A-homomorphism j : X Ä _A B ® X_A. Taking into account that M_i Ä _{A s}M_j = 0 for i ≠ s, the map j is defined in the following way:

(3.5)

Since M_i Ä _{A i}M_j is mapping into V_j, and V_r Ä _{A r}M_j is mapping into V_j, j defines a set of D_j-homomorphisms:

(3.6)

(3.7)

for i = 1, 2, ..., k; r, j = k + 1, ..., n.

Now one can define R(X_T(W)) = (M_i, V_r, _jj_i, _jy_r). Let X, Y be two right T(W)-modules, let a: X ® Y be a homomorphism, and let R(X) = (M_i, V_r, _jj_i, _jy_r), R(Y) = . Let's define a morphism from R(X) to R(Y). Since a is an A-homomorphism, a(M_i) Í N_i, a(V_r) Í W_r, i.e., a defines a family of -homomorphisms a_i: M_i ® N_i and a family of D_r-homomorphisms b_r: V_r ® W_r, which are the restrictions of a to M_i and V_r. Therefore one can set R(a) = {(a_i), (b_r)}. Since a is a T(W)-homomorphism,

(3.8)

and

(3.9)

for i = 1, 2, ..., k; r, j = k + 1, ..., n. Therefore R(a) is a morphism in the category R(W).

Conversely, let W = (F_i, _iM_j)_i,jÎI and there is given a representation M = (M_i, V_r, _jj_i, _jy_r). Then one can define P(M) in the following way:

(3.10)

We define an action of

(3.11)

on M_i by means of the projection A ® and an action of A on V_r by means of the projection A ® D_r. We define an action of Bⁿ on X by induction of j ⁽ⁿ⁾ : X Ä_A Bⁿ ® X as follows:

If a = {{a_i}, {b_r}} is a morphism of a representation M = (M_i, V_r, _jj_i, _jy_r) to a representation , X = P(M), Y = P(), then

(3.12)

is a T(W)-homomorphism and therefore P(a) = j.

It is not difficult to show that R, P are mutually inverse functors and they give an equivalence of categories Mod_r T(W) and (W).

Recall that an Artinian ring A is of finite representation type if A has only a finite number of indecomposable finitely generated right A-modules up to isomorphism.

A ring A is of (right) bounded representation type (see [3, 4]) if there is an upper bound on the number of generators required for indecomposable finitely presented right A-modules.

Denote by m(M_i) the minimal number of generators of an -module M_i, and denote by d_r = the dimension of vector space V_r over D_r. The dimension of a representation M = (M_i, V_r, _jj_i, _jy_r) is the number

(3.13)

Definition 3.14. An O-species W is said to be of bounded representation type if the dimensions of its indecomposable finite dimensional representations have an upper bound.

Corollary 3.15. An O-species W is of bounded representation type if and only if the tensor algebra T(W) is of bounded representation type.

Proof. If W is an O-species of bounded representation type, then there exists N > 0 such that dimM < N for any indecomposable finite dimensional representation M. Then for any finitely generated T(W)-module X we have m(X) < N₁, where N₁ is some fixed number depending on N, i.e. T(W) is a ring of bounded representation type. The converse also holds: if T(W) is a ring of bounded representation type, then W is an O-species of bounded representation type.

Corollary 3.16. Let W₁ be a D-species, which is a subspecies of a (D, O)-species W. If W is of bounded representation type, then W₁ is of finite type.

Proof. Since W is of bounded representation type, each of its subspecies is of bounded representation type as well. So W₁ is of bounded representation type, and, by corollary 3.15, its tensor algebra is of bounded representation type, as well. Since W₁ is a D-species, its tensor algebra is an Artinian ring. So it is of finite representation type, by [5]. Therefore, W₁ is also of finite representation type.

3. Conclusion

In this paper we introduced O-species and the tensor algebras corresponding to them. These O-species are some generalizations of species first introduced by Gabriel in [1]. We consider the notion of a representation of an O-species. In this paper we prove that the category of all representations of O-species W and the category of all right modules over a tensor algebra T(W) are naturally equivalent.

References

[1] Gabriel P., Indecomposable representations I, Manuscripta Math. 1972, 6, 71-103.

[2] Dlab V., Ringel C.M., On algebras of finite representation type, Journal of Algebra 1975, 33, 306-394.

[3] Warfield R.B., Serial rings and finitely presented modules, Journal of Algebra 1975, 37, 2, 187-222.

[4] Gubareni N., On right hereditary SPSD-rings of bounded representation type I, Scientific Research of the Institute of Mathematics and Computer Science 2012, 3(11), 57-70.

[5] Auslander M., Representation theory of Artin algebras II, Comm. Algebra 1974, 1, 269-310.