Algorithm of rebuilding a boundary of domain during creation of an optimal shape
Katarzyna Freus
,Sebastian Freus
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
 View in HTML format |
 Export citation |
@article{Freus_2016,
doi = {10.17512/jamcm.2016.1.02},
url = {https://doi.org/10.17512/jamcm.2016.1.02},
year = 2016,
publisher = {The Publishing Office of Czestochowa University of Technology},
volume = {15},
number = {1},
pages = {17--24},
author = {Katarzyna Freus and Sebastian Freus},
title = {Algorithm of rebuilding a boundary of domain during creation of an optimal shape},
journal = {Journal of Applied Mathematics and Computational Mechanics}
}TY - JOUR DO - 10.17512/jamcm.2016.1.02 UR - https://doi.org/10.17512/jamcm.2016.1.02 TI - Algorithm of rebuilding a boundary of domain during creation of an optimal shape T2 - Journal of Applied Mathematics and Computational Mechanics JA - J Appl Math Comput Mech AU - Freus, Katarzyna AU - Freus, Sebastian PY - 2016 PB - The Publishing Office of Czestochowa University of Technology SP - 17 EP - 24 IS - 1 VL - 15 SN - 2299-9965 SN - 2353-0588 ER -
Freus, K., & Freus, S. (2016). Algorithm of rebuilding a boundary of domain during creation of an optimal shape. Journal of Applied Mathematics and Computational Mechanics, 15(1), 17-24. doi:10.17512/jamcm.2016.1.02
Freus, K. & Freus, S., 2016. Algorithm of rebuilding a boundary of domain during creation of an optimal shape. Journal of Applied Mathematics and Computational Mechanics, 15(1), pp.17-24. Available at: https://doi.org/10.17512/jamcm.2016.1.02
[1]K. Freus and S. Freus, "Algorithm of rebuilding a boundary of domain during creation of an optimal shape," Journal of Applied Mathematics and Computational Mechanics, vol. 15, no. 1, pp. 17-24, 2016.
Freus, Katarzyna, and Sebastian Freus. "Algorithm of rebuilding a boundary of domain during creation of an optimal shape." Journal of Applied Mathematics and Computational Mechanics 15.1 (2016): 17-24. CrossRef. Web.
1. Freus K, Freus S. Algorithm of rebuilding a boundary of domain during creation of an optimal shape. Journal of Applied Mathematics and Computational Mechanics. The Publishing Office of Czestochowa University of Technology; 2016;15(1):17-24. Available from: https://doi.org/10.17512/jamcm.2016.1.02
Freus, Katarzyna, and Sebastian Freus. "Algorithm of rebuilding a boundary of domain during creation of an optimal shape." Journal of Applied Mathematics and Computational Mechanics 15, no. 1 (2016): 17-24. doi:10.17512/jamcm.2016.1.02
ALGORITHM OF REBUILDING A BOUNDARY OF DOMAIN DURING CREATION OF AN OPTIMAL SHAPE
Katarzyna Freus 1, Sebastian Freus 2
1
Institute of Mathematics, Czestochowa University of Technology, Częstochowa,
Poland
2 Institute of Computer and Information Science, Czestochowa
University of Technology, Częstochowa, Poland
katarzyna.freus@im.pcz.pl, sebastian.freus@icis.pcz.pl
Abstract. In order to achieve the desired topology we often have to remove material of the area considered. This work presents the author's algorithm which can be used in the reconstruction of the boundary of domain after elimination of a certain amount of material. The paper introduces some details about the procedure that allows one to achieve the expected shape of a domain. The topological-shape sensitivity method for the Laplace equation is used to obtain an optimal topology, whereas numerical methodology utilizes the boundary element method. In the conclusion of the paper the example of computation is shown.
Keywords: Laplace equation, boundary element method, heat transfer, topological-shape sensitivity method
1. Introduction
Paper [1] presented the theory and numerical experiment that led to achieving an optimal shape of domain using the topological derivative and the boundary element method. This work is a follow-up of the article [1] and focuses on the analysis of an algorithm which describes the rebuilding of a boundary of domain during the optimization process. From a numerical point of view, the algorithm of the boundary reconstruction is rather complicated. Taking into account the boundary linear elements, one is required to use double boundary nodes when the boundary conditions are changed. We also have to pay attention to an appropriate sequence of the boundary nodes. Namely, the numbering of the nodes on an external boundary should be anticlockwise, whereas the numbering of the nodes on an interior boundary must be clockwise. On the other hand, the material is progressively removed by putting the holes in correct places of the domain. The topological derivative gives the information on the opportunity to create a small hole in the domain of interest. Wherever the value of topological derivative is low enough, the material can be eliminated. In the paper the topological-shape sensitivity method is used as a procedure to calculate the topological derivative taking the total potential energy as a cost function [2, 3].
In this work, firstly the problem is formulated. Next, the algorithm of rebuilding the boundary is presented, then the example is shown. Finally, conclusions are expressed.
2. Formulation of the problem
The domain W bounded by
contour Γ = Γ1 ![]() Γ2 is considered. The Laplace equation
supplemented by the boundary conditions is taken into account [2-5]
Γ2 is considered. The Laplace equation
supplemented by the boundary conditions is taken into account [2-5]
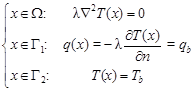 | (1) |
where x = (x1, x2) are the spatial coordinates, λ is the thermal conductivity, T (x) is the temperature, ∂T (x)/∂n denotes the normal derivative and n = [cosα1, cosα2] is the normal outward vector. Tb is the boundary temperature and qb is the boundary heat flux. On the holes created via Topological Derivative (DT), the Neumann boundary condition is prescribed, that is, q (x) = 0. In this case the expression for the topological derivative is the following
| (2) |
The aim of the work is to find the desired optimal topology of the domain considered using the iterative procedure which is carried out in the following steps:
1. Provide the initial domain Ω and the stop criterion.
2. Solve problem (1) using the BEM.
3. Calculate DT at internal points by means of e.g. (2).
4. Select the points with the lowest values of DT.
5. On the selected points create a hole.
6. Define the new domain Ωi (rebuild the boundary and mesh), where i is the i-th iteration.
7. Repeat the procedure until a given stop criterion is obtained.
As it was mentioned, problem (1) is solved by means of the BEM [1, 5]. Details of this method and the calculation of DT are described in [1-3]. Steps 5 and 6 will be discussed in the next section.
3. Algorithm of rebuilding the boundary
In this part of our paper we deal with the problem of shape modification of area. In each iteration, on the selected points where DT is low enough, the material is eliminated by inserting a hole with the centre point P0 = (x0, y0). It is important to mention that the area of holes should be equal to about 2% of the area of the whole domain. The boundary of the openings is divided into 6 linear boundary elements (see Fig.1). In order to automate the process, it is assumed that the side length of a regular hexagon is approximately equal to the length of the boundary element (ds).
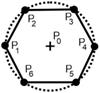
Fig. 1. Hexagonal hole
Coordinates of the hexagon vertices are the following:
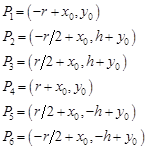 | (3) |
where r is a radius of the hole, while
| (4) |
For each node formed by the regular hexagon vertices Pi = (xiP, yiP) , i = 1,2,…6 the nearest boundary node is searched using the formula
| (5) |
where Wj = (xjW, yjW) and n are the coordinates and the number of the boundary nodes, respectively. Next, the following criterion is considered (the so-called “contact criterion”)
| (6) |
If criterion (6) is satisfied, then it is assumed that i-th the hexagon node keeps in contact with j-th the boundary node, ds means the length of the boundary element.
Information about number of nodes which satisfy criterion (6) or not is stored in two separate matrices: CM (contact matrix) or NCM (not contact matrix). The matrix CM also includes knowledge about the distance of nodes and the type of boundary conditions in these nodes. For example, in Figure 2 nodes 2 and 34, 3 and 35 satisfy criterion (6) and 1 and 33, 4 and 36 do not satisfy it. Nodes 33, 1, 6, 5, 4 and 36 must be spliced to create the new outline of the domain.

Fig. 2.
If the matrix CM is empty (neither of the nodes are in contact) then we can create a new hole prescribing the Neumann boundary condition q = 0 on its boundary (see Fig. 3). Now, we discuss some cases concerning connecting the hexagon nodes with the boundary ones. An analysis is conducted taking into account the successive nodes of the hexagon. The first case is shown in Figure 2. An increase is noticed in the numbering of boundary nodes and an increase in the numbering of hole nodes. The contact criterion is satisfied for 2 and 34, 3 and 35 nodes. In Figure 4, the numbering of hole nodes is increasing while the numbering of the boundary ones is decreasing. The nodes 5 and 3, 6 and 2 fulfill criterion (6).
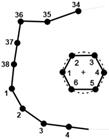
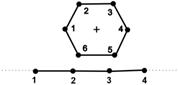
Fig. 3. Fig. 4.
Further considerations involve doing a sorting of the nodes which satisfy the contact criterion. The rows of the matrix are sorted taking into account the numbering of the boundary nodes. It is worth noting that the first column contains the hexagon's node number and the second one the node number of the boundary. For instance, two columns of the CM before sorting are the following (see Fig. 4).
| (7) |
and after sorting
| (8) |
Sometimes to obtain the correct sorting we need to introduce the so-called substitute numbering. It is done when both the first and the last node of the hexagon satisfy criterion (6). To the nodes numbered from 1, we should add 10 (this means that we replace 1 by 11, 2 by 12, etc.).
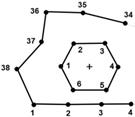
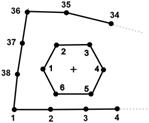
Fig. 5. Fig. 6.
For example, taking Figure 5 the contact matrix is the following:
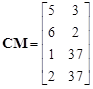 | (9) |
Next, in the third column of this matrix, the substitute numbering is introduced. Hence
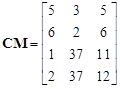 | (10) |
Since two vertices of the hexagon keep in contact with the same boundary node, the procedure of a two-level sort is used. Firstly, matrix (10) is ordered ascendingly taking into account the boundary node number and then descendingly in regard to the third substitute column. Finally, the matrix CM is of the form
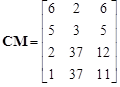 | (11) |
In the case when the boundary nodes contact, including the first and the last boundary node at the same time, then the CM is divided into two of the following matrices
| (12) |
The next step is finding a minimum and maximum number of the hexagon node and the boundary node in matrices CM1 and CM2 (see expressions (12)).
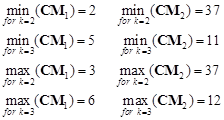 | (13) |
where k is the appropriate number of a column in the matrices. The nodes that are not in contact create a new contour of domain. It is done by searching for a minimum and maximum of the hexagon nodes. The boundary nodes from 1 to min(CM1) and from 1 to min(CM2) are removed. The different case is when all of the hexagon nodes keep in contact (see Fig. 6). Then a closed contour is obtained using the new boundary element by connecting boundary nodes 4 and 34.
To check the effectiveness of the proposed algorithm, the example of computations was carried out.
4. Numerical example
The square domain of dimensions 0.1´0.1 m, shown in Figure 7, has been considered. Thermal conductivity equals λ = 1 W/(m∙K). The boundary conditions have been marked in Figure 7. The initial boundary has been divided into 34 linear boundary elements. The grid of 53 internal nodes has been used. On the holes created via topological derivative, the Neumann condition (q = 0) is prescribed. Holes with r = 0.05 were used and the iterative procedure was stopped when 50% of material from the initial domain was eliminated. Figure 8 illustrates the temperature distribution in the domain considered, while Figure 9 presents the topological derivative obtained in the first iteration (i = 0).

Fig. 7. Domain considered
Due to the symmetry of the problem, only half of domain is taken into account.

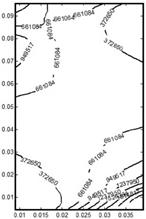
Fig. 8. Temperature distribution at i = 0 Fig. 9. Topological derivative at i = 0
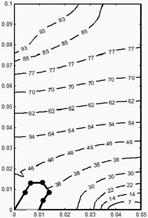
Fig. 10. Temperature distribution at i = 1

Fig. 11. Final result
Figure 10 shows the temperature distribution at i = 1. The final result was obtained at iteration i = 21, as can be seen in Figure 11.
5. Conclusions
In the present work, the topological derivative is used to obtain an optimal shape of domain. This paper focuses on describing the algorithm of rebuilding the boundary of domain. It presents some details concerning creating holes inside the area and removing the nodes. To inspect the correctness of the algorithm, the example of computation was conducted. The results of the study show good agreement with the available literature.
References
[1] Freus K., Freus S., Determination of an optimal shape of domain using the topological derivative and Boundary Element Method, Journal of Applied Mathematics and Computational Mechanics 2014, 13(4), 41-48.
[2] Navotny A.A., Feijoo R.A., Taroco E., Padra C., Topological-shape sensitivity analysis, Computer Methods in Applied Mechanics and Engineering 2003, 192, 803-829.
[3] Marczak R.J., Topology optimization and boundary elements - a preliminary implementation for linear heat transfer, Engineering Analysis with Boundary Elements 2007, 31, 793-802.
[4] Anflor C.T.M., Marczak R.J., Topological sensitivity analysis for two-dimensional heat transfer problems using the Boundary Element Method, Optimization of Structures and Components Advanced Structured Materials 2013, 43, 11-33.
[5] Brebbia C.A., Dominguez J., Boundary Elements. An Introductory Course, CMP, McGraw-Hill Book Company, London 1992.


